Visualizing Recursion

February 20, 2013

It seems that when the concept of recursion is introduced, a lot of people (including myself) have a hard time to understand it. Although, it is a powerful technique that is used in important algorithms. In addition, recursion often leads to simple and straightforward solutions.

I think one way of making things more clear is to visualize the process that is generated by a recursive algorithm.

Fibonacci Numbers

The classical example for introducing recursion is Fibonacci numbers. Consider this implementation in Python:

def fib(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fib(n - 1) + fib(n - 2)

What is interesting about this algorithm is that it generates a process with a tree structure. This is illustrated in the following.

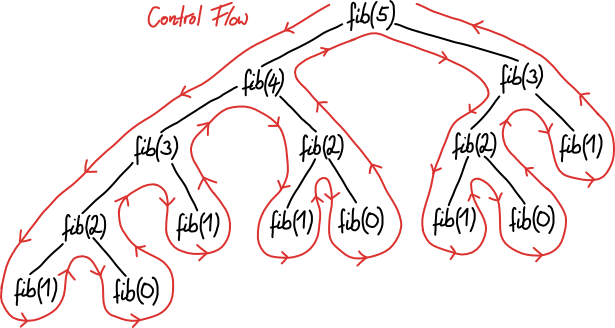
Fibonacci Process

Just by looking at the source code it is hard to reason about its generated process. In contrast, I think the illustration helps.

The picture also shows why this naive implementation is quite slow. A large number of function calls are computed multiple times.

Merge Sort

Another classical recursive algorithm is Merge sort. It is a divide and conquer algorithm that recursively breaks the input down into smaller problems and merges it back in sorted order. The algorithm is implemented like this (full implementation is available here):

def mergesort(lst):
    if len(lst) < 2:
        return lst
    middle = len(lst) / 2
    left = mergesort(lst[:middle])
    right = mergesort(lst[middle:])
    return merge(left, right)

The generated process of sorting 9, 1, 4, 6, 3, 2, 7, 8 is shown below.

Merge Sort Process

Constructing All Permutations

The problem of constructing all permutations of a string can be solved recursively. For instance, this implementation:

def permutations(string, rest):
    if len(rest) == 0:
        return [string]

    result = []
    for i in xrange(len(rest)):
        next_rest = [rest[j] for j in xrange(len(rest)) if j != i]
        result.extend(permutations(string + rest[i], ''.join(next_rest)))
    return result

produces the following process for “abc”.

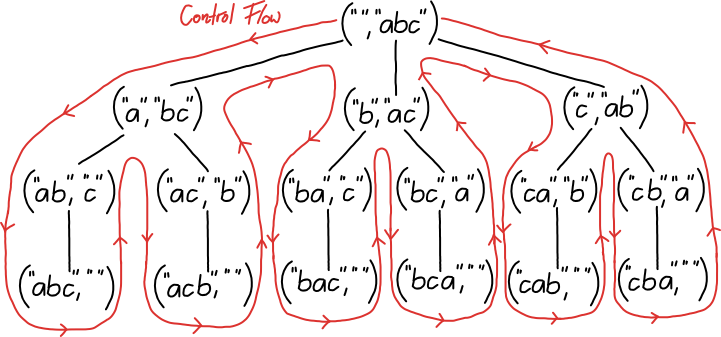
Permutations Process

Moreover, the resulting permutations of “abc” reside at the leaves of the process tree: “abc”, “acb”, “bac”, “bca”, “cab” and “cba”.

Conclusion

Of course, there are different strategies that help with understanding recursive processes. I think visualizing the process of a recursive algorithm is very helpful. Especially in the beginning.